EL MUNDO EN LA ESTADISTICA

domingo, 16 de octubre de 2011

Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de la probabilidad se requiere conocer el número de elementos que forman parte del espacio muestral, estos se pueden determinar con la construcción del diagrama de árbol.

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de esta ramas se conoce como rama de primera generación.

En el final de cada rama de primera generación se constituye a su vez, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta que la construcción de un árbol no depende de tener el mismo número de ramas de segunda generación que salen de cada rama de primera generación y que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

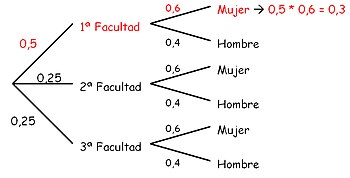
Existe un principio sencillo de los diagramas de árbol que hace que éstos sean mucho más útiles para los cálculos rápidos de probabilidad: multiplicamos las probabilidades si se trata de ramas adyacentes (contiguas), el ejemplo de alumna de la primera facultad, o bien las sumamos si se trata de ramas separadas que emergen de un mismo punto, el ejemplo de encontrar un alumno.

Ejemplos

Una universidad tiene de tres facultades:

La 1ª con el 50% de estudiantes.
La 2ª con el 25% de estudiantes.
La 3ª con el 25% de estudiantes.

Las mujeres están repartidas uniformemente, siendo un 60% del total en cada facultad.

Árbol con el planteamiento del problema.

¿Probabilidad de encontrar una alumna de la primera facultad?

Árbol con la probabilidad de encontrar una mujer en la primera facultad.

$P(alumna \ de \ la \ 1^a \ facultad) = 0,5 \cdot 0,6 = 0,3$

¿Probabilidad de encontrar un alumno varón?

Árbol con la probabilidad de encontrar un varón en la universidad.

$P(alumno \ var\acute{o}n) = 0,5 \cdot 0,4 + 0,25 \cdot 0,4 + 0,25 \cdot 0,4= 0,4$ pero también podría ser lo contrario.

[Relación con probabilidad condicionada

Esta herramienta esta fundamentada en el cálculo de probabilidades condicionadas.

Por ejemplo podemos identificar el 0,6 que encotramos en la rama que va de 1ª facultad a mujer como la siguiente probabilidad condicionada:

$P(mujer \mid 1^a \ facultad)=0.6$

También esta herramienta se relaciona con algunos teoremas de la probabilidad condicionada

El segundo cálculo que hemos realizado, se corresponde con la aplicación del teorema de la Probabilidad Total

Dado que las tres facultades forman una partición del espacio muestral podemos indicar este cálculo como:

$\scriptstyle P(alumno \ var\acute{o}n)=P(var\acute{o}n \mid 1^a \ facultad) \cdot P(1^a \ facultad)+P(var\acute{o}n \mid 2^a \ facultad) \cdot P(2^a \ facultad)+P(var\acute{o}n \mid 3^a \ facultad) \cdot P(3^a \ facultad)$

$P(alumno \ var\acute{o}n)=0.5 \cdot 0.4+0.25 \cdot 0.4+0.25 \cdot 0.4=0.4$

domingo, 25 de septiembre de 2011

CONTEO Y PROBABILIDAD

TÉCNICAS DE CONTEO

Se estudian en este aparte algunos técnicas especiales que facilitan el trabajo de contar los casos favorables y posibles que definen la medida de probabilidad.

PRINCIPIOS BASICOS DEL CONTEO
Sea un experimento que se tiene que realizar en K diferentes etapas, cada una se puede hacer de ni formas distintas, entonces el experimento completo puede hacerse en:

formas.

Ejemplos
Las maneras diferentes de viajar de una ciudad A a otra C pasando por una B, asumiendo que hay 3 alternativas para ir de A a B, y 4 de B a C
El número total de formas diferentes de viajar de A hasta C es: n $_{1}$ x n $_{2}$ = 3 x 4 = 12 El número total de las placas de los carros en Colombia, si se asumieran 3 letras de las 28 y 3 dígitos de los 10 se puede calcular como:
n $_{1}$ x n $_{2}$ x n $_{3}$ x n $_{4}$ x n $_{5}$ x n $_{6}$ = 10 $^{3}$ * 28 $^{3}$ = 21.952.000
con n $_{i}$ :número de formas de colocar el digito i, i=1, 2, 3
n $_{J}$ :número de formas de colocar la letra J, J=4, 5, 6

FUNDAMENTOS DE LA TEORÍA DE LA PROBABILIDAD

PROBABILIDAD CLÁSICA
Sea un experimento un espacio de resultados (S), con n resultados igualmente posibles en el cual define un evento A con nA resultados posibles en él, entonces

PROBABILIDAD FRECUENTISTA
Repetición de un experimento bajo las mismas condiciones muchas veces y repetirlo casi hasta que llegue a la probabilidad clásica, entonces

PROBABILIDAD SUBJETIVA
Un punto de vista alternativo que actualmente ha tenido popularidad es interpretar las probabilidades como evaluaciones personales o subjetivas. Tales probabilidades expresan una creencia sobre las incertidumbres involucradas, y se aplican especialmente cuando poca o ninguna evidencia; así que no hay otra opción que considerar evidencias paralelas (indirectas), conjeturas fundamentadas y quizás intuición u otros factores subjetivos.
Entonces

Probabilidad = O !! el evento no ocurrirá

Probabilidad = 1 !! seguro el evento ocurre

MEDIDAS DE PPOSICION Y DE FORMA

Medidas de Posición

Son indicadores usados para señalar que porcentaje de datos dentro de una distribución de frecuencias superan estas expresiones, cuyo valor representa el valor del dato que se encuentra en el centro de la distribución de frecuencia, por lo que también se les llama " Medidas de Tendencia Central ".

Pero estas medidas de posición de una distribución de frecuencias han de cumplir determinadas condiciones para que lean verdaderamente representativas de la variable a la que resumen. Toda síntesis de una distribución se considerara como operativa si intervienen en su determinación todos y cada uno de los valores de la distribución, siendo única para cada distribución de frecuencias y siendo siempre calculable y de fácil obtención. A continuación se describen las medidas de posición más comunes utilizadas en estadística, como lo son:

Cuartiles: Hay 3 cuartiles que dividen a una distribución en 4 partes iguales: primero, segundo y tecer cuartil.
Deciles: Hay 9 deciles que la dividen en 10 partes iguales: (primero al noveno decil).
Percentiles: Hay 99 percentiles que dividen a una serie en 100 partes iguales: (primero al noventa y nueve percentil)

Medidas de Forma

Una vez iniciado el análisis estadístico de sinterización de la información, para lo cual hemos estudiado las medidas de posición y dispersión de la distribución de una variable, necesitamos conocer más sobre el comportamiento de la misma. No podemos basar nuestras conclusiones únicamente en expresiones que vengan dadas en términos de medidas de posición y dispersión. Si bien intentamos globalizar el comportamiento del colectivo que sea objeto de nuestro estudio, para lo cual las medidas de posición son nuestro mejor instrumento, no debemos proceder a una intrepretación que implique un comportamiento de todos los elementos del colectivo uniformemente constante e igual a la medida de posición en cuestión con un error dado por la correspondiente medida de dispersión. Este error o disparidad se hace más ostensible al analizar la representación gráfica de la distribución. Pues bien, las medidas de forma de una distribución se basan en su representación grafica, sin llegar a realizar la misma.

TOPICO 4° PERIODO

TOPICO IV P
7°A 9°
INTERPRETACION DE CONTEO Y PROBABILIDAD
CONTEO
DIAGRAMA DE ARBOL
PROBABILIDAD
LANZAMIENTO
10°
TENDENCIA
EJERCICIOS DE APLICACION
GRAFICOS CIRCULARES
DATOS AGRUPADOS
CONTEO
11°APLICACION A LAS MEDIDAS DE POSICION Y FORMA
EJERCICIOS DE APLICACION
GRAFICAS CIRCULARES
DATOS AGRUPADOS

domingo, 31 de julio de 2011

MEDIDAS DE TENDENCIAS GRADO 11

ACTIVIDAD
GRADO: 11° A, B Y C
Con lo observación de los videos respondo:
1) ¿Cómo se halla el rango? Da ejemplo
2) ¿Cómo se halla la media geométrica?
3) Cual es la formula y el símbolo de la media geométrica o promedio?
Ejercicio 2...1. En el siguiente conjunto de números, se proporcionan los pesos (redondeados a la libra más próxima) de los bebés nacidos durante un cierto intervalo de tiempo en un hospital:
4, 8, 4, 6, 8, 6, 7, 7, 7, 8, 10, 9, 7, 6, 10, 8, 5, 9, 6, 3, 7, 6, 4, 7, 6, 9, 7, 4, 7, 6, 8, 8, 9, 11, 8, 7, 10, 8, 5, 7, 7, 6, 5, 10, 8, 9, 7, 5, 6, 5.
1. Construir una distribución de frecuencias de estos pesos.
2. Encontrar las frecuencias relativas.
3. Encontrar las frecuencias acumuladas.
4. Encontrar las frecuencias relativas acumuladas.
5. Dibujar un histograma con los datos de la parte a.
6. ¿Por qué se ha utilizado un histograma para representar estos datos, en lugar de una gráfica de barras?
7. Calcular las medidas de tendencia central.
8. Calcular las medidas de dispersión.
9. Calcular las medidas de forma.
10. ¿Es esta una distribución sesgada? De ser así, ¿en qué dirección?
11. Encontrar el percentil 24.
Ejercicio 2...2. A continuación se dan los resultados obtenidos con una muestra de 50 universitarios. la característica es el tiempo de reacción ante un estímulo auditivo:
0,110 0,110 0,126 0,112 0,117 0,113 0,135 0,107 0,122
0,113 0,098 0,122 0,105 0,103 0,119 0,100 0,117 0,113
0,124 0,118 0,132 0,108 0,115 0,120 0,107 0,123 0,109
0,117 0,111 0,112 0,101 0,112 0,111 0,119 0,103 0,100
0,108 0,120 0,099 0,102 0,129 0,115 0,121 0,130 0,134
0,118 0,106 0,128 0,094 0,1114
1. ¿Cuál es la amplitud total de la distribución de los datos?
2. Obtenga la distribución de frecuencias absolutas y relativas.
3. Obtenga la distribución de frecuencias acumuladas, absolutas y relativas, con los intervalos anteriores.
4. Calcular la media y la varianza con los intervalos del apartado b y después calcúlense las mismas magnitudes sin ordenar los datos en una tabla estadística. ¿Con qué método se obtiene mayor precisión?
5. Dibuje el polígono de frecuencias relativas.
6. Dibuje el polígono de frecuencias relativas acumuladas.
Ejercicio 2...3. Con el fin de observar la relación entre la inteligencia y el nivel socioeconómico (medido por el salario mensual familiar) se tomaron dos grupos, uno formado con sujetos de cociente intelectual inferior a 95 y otro formado por los demás; De cada sujeto se anotó el salario mensual familiar. Teniendo en cuenta los resultados que se indican en la tabla:
Nivel socioeconómico Sujetos con CI < 95 Sujetos con
Intervalos Frecuencia Frecuencia
10 o menos 75 19
10 - 16 35 26
16 - 22 20 25
22 - 28 30 30
28 - 34 25 54
más de 34 15 46
1. Dibuje un gráfico que permita comparar ambos grupos.
2. Calcule las medidas de tendencia central para aquellos sujetos con CI < 95.
3. Calcular las medidas de dispersión para aquellos sujetos con .
Ejercicio 2...4. Un estudio consistió en anotar el número de palabras leídas en 15 segundos por un grupo de 120 sujetos disléxicos y 120 individuos normales. Teniendo en cuenta los resultados de la tabla
de palabras leídas Disléxicos nD Normales nN
25 o menos 56 1
26 24 9
27 16 21
28 12 29
29 10 28
30 o más 2 32
Calcule:
1. Las medias aritméticas de ambos grupos.
2. Las medianas de ambos grupos.
3. El porcentaje de sujetos disléxicos que superaron la mediana de los normales.
4. Compare la variabilidad relativa de ambos grupos.
Ejercicio 2..5. La tabla siguiente muestra la composición por edad, sexo y trabajo de un grupo de personas con tuberculosis pulmonar en la provincia de Vizcaya en el año 1979:
Edad Trabajadores No trabajadores Totales
Varón Mujer Total Varón Mujer Total Varón Mujer Total
14-19 2 1 3 25 40 65 27 41 68
19-24 10 4 14 20 36 56 30 40 70
24-29 32 10 42 15 50 65 47 60 107
29-34 47 12 59 13 34 47 60 46 106
34-39 38 8 46 10 25 35 48 33 81
39-44 22 4 26 7 18 25 29 22 51
1. Representar gráficamente la distribución de frecuencias de aquellas personas trabajadoras que padecen tuberculosis.
2. Representar gráficamente la distribución de frecuencias de los varones no trabajadores que padecen tuberculosis.
3. Representar gráficamente la distribución de frecuencias del número total de mujeres que padecen tuberculosis.
4. ¿Cuál es la edad en la que se observa con mayor frecuencia que no trabajan los varones? ¿Y las mujeres? Determinar asimismo la edad más frecuente (sin distinción de sexos ni ocupación).
5. ¿Por debajo de qué edad está el 50% de los varones?
6. ¿Por encima de qué edad se encuentra el 80% de las mujeres?
7. Obtener la media, mediana y desviación típica de la distribución de las edades de la muestra total.
8. Estudiar la asimetría de las tres distribuciones.
Ejercicio 2...6. En una epidemia de escarlatina, se ha recogido el número de muertos en 40 ciudades de un país, obteniéndose la siguiente tabla:
de muertos 0 1 2 3 4 5 6 7
Ciudades 7 11 10 7 1 2 1 1
1. Representar gráficamente estos datos.
2. Obtener la distribución acumulada y representarla.
3. Calcular media, mediana y moda.
4. Calcular la varianza y la desviación típica.
5. Porcentaje de ciudades con al menos 2 muertos.
6. Porcentaje de ciudades con más de 3 muertos.
7. Porcentaje de ciudades con a lo sumo 5 muertos.